输入：n个数的一个序列<a1,a2,...,an> (A[1..n]) 输出：输入序列的一个排序<b1,b2,...,bn>，满足b1≤b2≤...≤bn。

思想

分治法： 1. 分解：数组A[p..r]被划分为两个（可能为空）子数组A[p..q-1]和A[q+1..r]，使得A[p..q-1]中的每一个元素都小于等于A[q]，而A[q]也小于等于A[q+1..r]中的每个元素。其中，计算下标q也是划分过程的一部分(PARTITION(A, p, r)) 2. 解决：通过递归调用快速排序，对子数组A[p..q-1]和A[q+1..r]进行排序 3. 合并：因为子数组都是原址排序，所以不需要合并操作。即，数组A[p..r]已经有序

参考：Wiki百科：快速排序

实现

伪代码

# 初识调用：QUICKSORT(A, 1, A.length)
QUICKSORT(A, p, r)
    if p < r
        q = PARTITION(A, p, r)
        QUICKSORT(A, p, q-1)
        QUICKSORT(A, q+1, r)
# 对子数组A[p..r]进行原址重排。O(n), n=r-p+1
PARTITION(A, p, r)
    x = A[r] # 选择最后一个元素作为pivot
    i = p - 1 # i表示比pivot小的值的最大下标，即A[p..i]都不大于pivot值
    for j = p to r-1 # 从头开始扫描数组。A[i+1, j-1]都大于pivot值
        if A[j] <= x # 若当前元素不大于pivot的值，则把其与A[i+1]交换
            i = i + 1
            exhange A[i] with A[j]
    exhange A[i+1] with A[r]
    return i+1

1. Python实现（升序）

def PARTITION(A, p, r):
    x = A[r]
    i = p - 1
    for j in range(p,r):
        if A[j]<=x: # 如果将这里修改为A[j] > x，则为降序排列
            i += 1
            A[i],A[j] = A[j], A[i]
    A[i+1], A[r] = A[r], A[i+1]
    return i+1
def QUICKSORT_ASC(A, p, r):
    if p < r:
        q = PARTITION(A, p, r) # 此时下标为q的值已经确定了，后面的排序应该排除它
        QUICKSORT_ASC(A, p, q-1)
        QUICKSORT_ASC(A, q+1, r)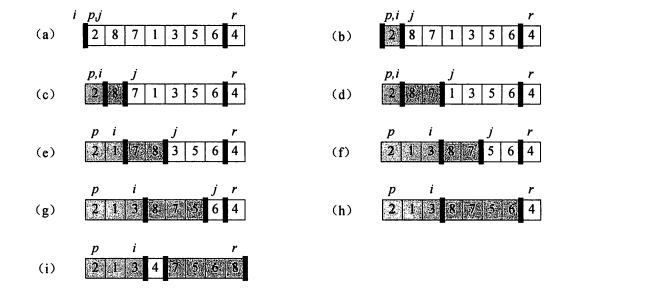

# 图片说明

## 复杂度 1. 空间复杂度：O(1), in-place排序 2. 最差时间复杂度：O(n^2), 平均/最优时间复杂度：O(nlgn) 最差时间复杂度出现在每次划分都包含了n-1个元素和0个元素；最优时间复杂度出现在每次划分都包含了n/2个元素和n/2个元素

注意

改进：使用随机抽样确定pivot，然后再与最后一个元素交换

RANDOMIZED-PARTITION(A, p, r)
    i = RANDOM(p, r)
    exchange A[i] and A[r]
    return PARTITION(A, p, r)

∞

九大排序算法及其Python实现之快速排序

思想

实现

注意